OCEAN MODELLING AND FLUIDS GROUP
Research Topics
Here you can find some of the research projects we have been involved in to get a sense of the kind of approach we take and tools we use, roughly organised by theme.
Eddy parameterisation + Ocean modelling
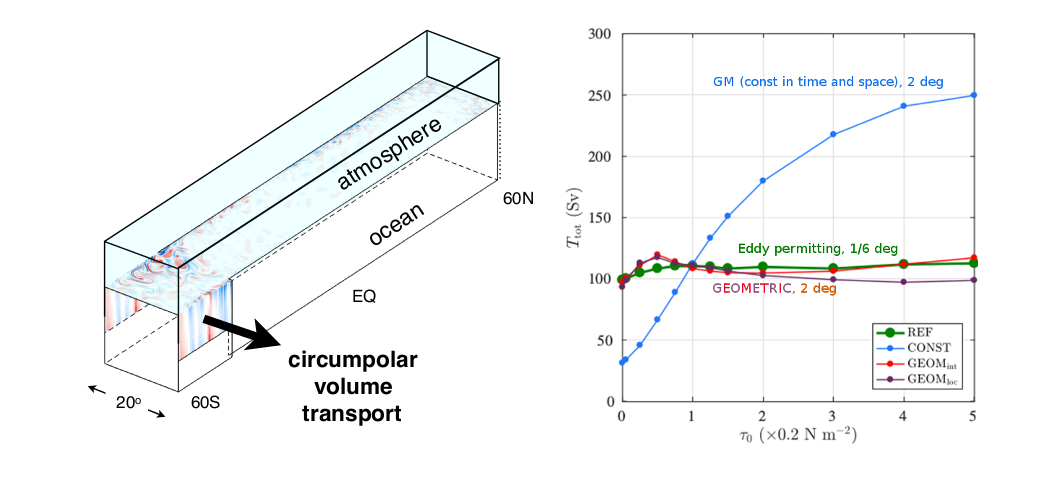A part of studying eddy/wave-mean flow interaction concerns parameterisation, i.e. representation of sub-grid physics in models. At present we have a focus on eddy energy constrained mesoscale eddy parameterisations associated with baroclinic instabilities. In particular, we concentrate on developing, implementing and assessing the impact of the GEOMETRIC scheme. So far we have GEOMETRIC implemented in MITgcm (w/ James Maddison), NEMO (w/ Gurvan Madec) and MOM6 (NCAR branch, largely thanks to Scott Bachman).
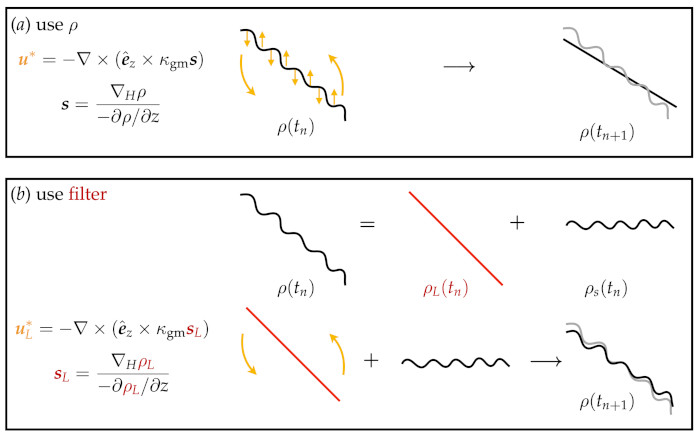One topic we are looking into is on applying parameterisations in eddy permitting resolutions, where there is some sentiment suggesting GEOMETRIC surely cannot function in that regime (because it is a GM-based scheme so should have issues with damping explicit eddies, e.g. video where GM-based schemes are switched on at model year 500). Revisiting the original reason on why GM schemes damp the explicit fluctuations, we have a proposal that circumvents the problem. Current work is on further adapting the proposal and testing these out in various settings to evaluate the associated skill and/or shortfalls.
Some of the research here overlaps with inverse / data-driven methods, and the more theoretical projects.
Inverse / data-driven / machine learning problems
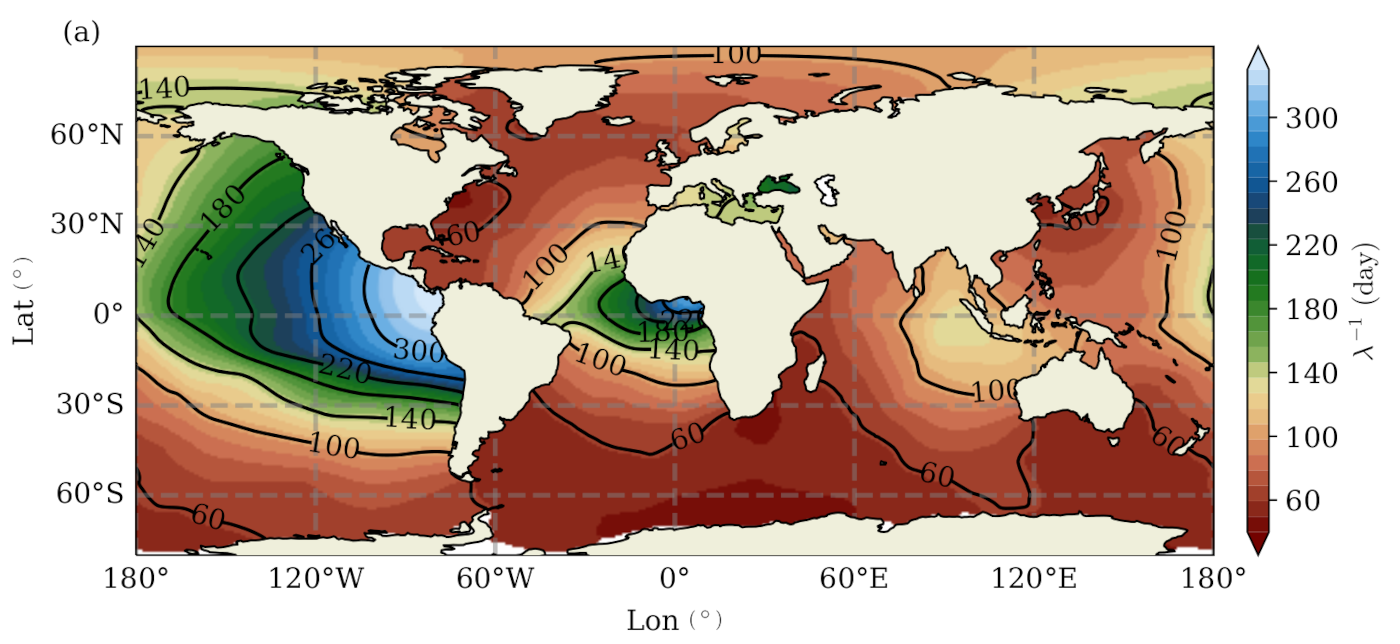One piece of work motivated by the work on eddy parameterisation and GEOMETRIC is on parameter inference. In some previous work we found that the performance of GEOMETRIC crucially depends on the eddy energy dissipation parameter, but this parameter depends on a multitude of different dynamical processes. As a way to constrain the distribution and magnitudes of this parameter, we ask the reverse question: "if we ended up with what we observe, what should we have chosen in the first place to have got here?" This is a standard inference type calculation, and a way we did it is given in the figure here, solving an optimisation of the kind we did at some point for inferring the eddy diffusivity.
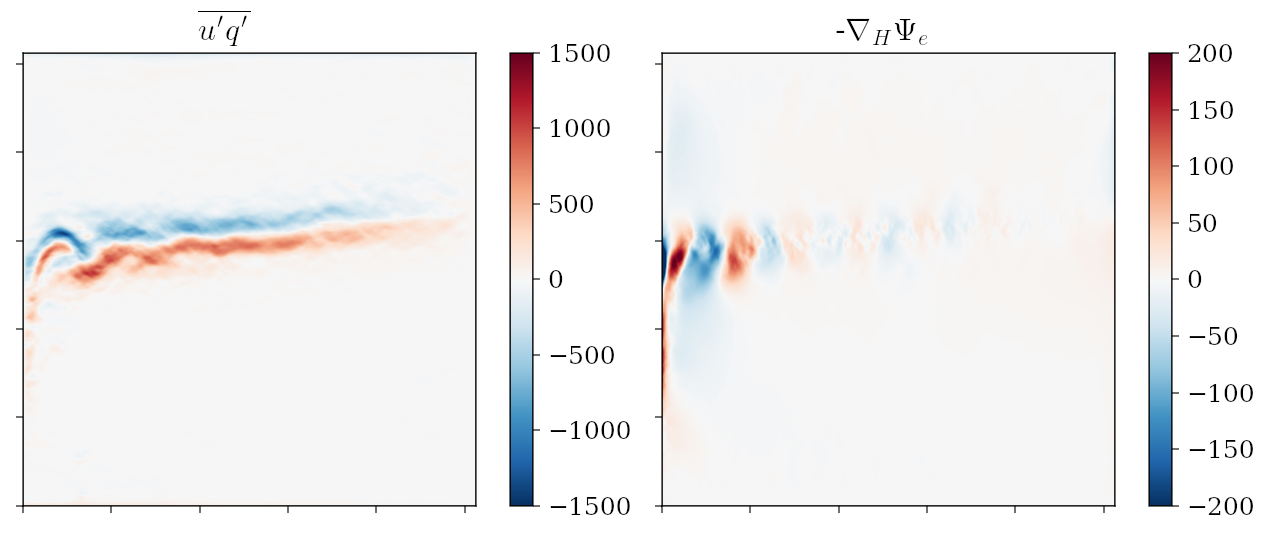Another topic we are looking into is on the application of machine learning algorithms for learning about eddy flux and mean state relations, which is central to eddy parameterisation. A technical complication however arises from the fact that rotational fluxes play no role in the dynamics. The questions are how do we get rid of it, do we actually need to get rid of it, and if so what benefits does doing so afford? We are also looking to do similar things, but with a dynamical model constraining the evolution of the model (cf. what is done in state estimates as in ECCO, or in data assimilation methodologies such as 4DVAR).
Chaotic/turbulent stirring and transport
Theoretical problems (mostly fluids)
We have a particular focus on shear instabilities, particularly with baroclinic instabilities (in the geophysical as well as astrophysical context), and interaction of waves as an explanation to instability. One current focus is on baroclinic equilibration and baroclinic lifecycles. While in some sense these are rather old topics, open and fundamental questions remain, such as "can we predict the equilibration state given initial state", or "what are the mechanisms governing equilibration", even within an at-first-sight-simple spindown problem in a quasi-geostrophic two layer system. Other questions, such as the extent of quasi-linear control on the nonlinear dynamics, and mechanistic explanations of the barotropic governor mechanism, are also being pursued.
Another topic we are looking into is that of baroclinic instability over slopes, which has applications for ocean eddy parameterisations. It is generally understood that baroclinic instability is suppressed over the ocean continental shelves and slopes, and in turn suppressing mesoscale eddies in these regions. From a parameterisation point of view this suggests we need to suppress the mesoscale parameterisation scheme over these regions, but how do we do this in a physically informed way, and what are the consequences if we don't do it properly? We are also re-examining aspects of the instability process over the slopes, to understand the physical mechanism leading to the suppression of instability and the implied feedback onto the mean state.
How would the equivalent problem for a ionised fluid behave, i.e. within the magnetohydrodynamic (MHD) description? In the case of the Earth's core, stellar interiors or generally in astrophysics, the fluid is electronically conducting and therefore influenced by magnetic forces, leading additional phenomena. The hydrodynamic studies provide a valuable reference for the analogous MHD problems, and possible vice-versa. Past research includes equilibration of MHD shear flow instabilities, and explanation of the instabilities in terms of wave interaction. One piece of recent research involves formal analogies to do with GFD and plasma waves. The PI maintains an interest in shear instabilities within the framework of Hamiltonian fluid mechanics and symmetry breaking aspects (in both the GFD and MHD context) should a potential student/post-doc want to look into more theoretical topics.